Hola amigos, empezaremos desde lo más básico, función lineal.
Ecuaciónde la recta:
Y= mx + b
Siendo M la pendiente
Siendo B la ordenada al origen (el valor de Y que es cuando x vale “0″[cero], cortando al eje y)
también se puede escribir de la siguiente manera, Segmentariamente:
Función Lineal ecuación Segmentaría
1 = x/a_1 + y/b_1
Siendo a_1 donde se corta al eje X
Siendo b_1 donde se corta al eje Y
Ejemplos:
1ª caso : Y = 2x + 5
tenemos que la pendiente sera 2 y la ordenada al origen 5
2ª caso : 1 = x/10 + y/15tenemos que corta al eje x en 10 y al eje y en 15, entonces uniendo esos 2 puntos que serian
para x (10 ; 0) e Y (0 ; 15) entonces podemos unir estos dos puntos teniendo nuestra recta que sera la representación gráfica de nuestra función.
¿ como obtener la pendiente de una recta ?
Bueno yo generalmente uso esta formula sencilla y fácil de acordarnos para averiguar la pendiente al tener 2 puntos como es el segundo caso.
Formula:
m= (y1 – y0) / (x1 – x0)
resolviendo esto para cualquier función lineal obtendremos la pendiente
Ejemplo para a ver si nos queda mas claro
Tengo los puntos ( 0 ; 5) y (2 ; 10)
entonces nuestro y1 y y0 serian 5 y 10 respectivamente
y nuestros x1 y x0 serian 0 y 2 respectivamente
Entonces obtendremos que:
M = (5 – 10) / (0 – 2) = 5/2
esta bien tenemos ya la M de la función y ahora como sacar B (ordenada al origen)para obtener la ecuación: y = mx + b
como el valor de M lo sabemos solamente le daremos un valor de un punto que sepamos de Y y X
pudiendo hacer la siguiente ecuación
y1 = M.x1 + b
como y1, x1 y m sabemos los valores entonces reemplazamos teniendo
y1 = 5 , x1= 0 y m = 5/2
entonces
5 = 5/2 . 0 + b
entonces 5 = b
entonces ya tenemos que nuestra función a partir de 2 puntos es
Y = 5/2.x + 5.
¿ Que dominio e imagen tienen estas funciones lineales ?
El dominio de estas funciones Lineales seran “Todos los Reales”
La imagen de estas funciones Lineales seran tambien “Todos los Reales”
porque podemos darle a X cualquier valor y siempre obtendremos un valor diferente de Y.
lunes, 15 de noviembre de 2010
Definiciones respecto de un triángulo rectángulo
Para definir las razones trigonométricas del ángulo: α, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa
Para definir las razones trigonométricas del ángulo: α, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo α , en cuyo caso se trata de triángulos semejantes.
- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto (a) es el lado opuesto al ángulo que queremos determinar.
- El cateto adyacente (b) es el lado adyacente al ángulo del que queremos determinar.
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa
Para definir las razones trigonométricas del ángulo: α, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto (a) es el lado opuesto al ángulo que queremos determinar.
- El cateto adyacente (b) es el lado adyacente al ángulo del que queremos determinar.
Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa
3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente
4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:
razones trigonometricas
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen (sin) | |
| Coseno | cos | |
| Tangente | tan | |
| Cotangente | cot | |
| Secante | sec | |
| Cosecante | csc (cosec) |
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen (sin) | |
| Coseno | cos | |
| Tangente | tan | |
| Cotangente | cot | |
| Secante | sec | |
| Cosecante | csc (cosec) |
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen (sin) | |
| Coseno | cos | |
| Tangente | tan | |
| Cotangente | cot | |
| Secante | sec | |
| Cosecante | csc (cosec) |
martes, 2 de noviembre de 2010
funcion cuadratica
Una función de la forma:
f (x) = a x ² + b x + c |
con a, b y c pertenecientes a los reales y a ¹ 0, es una función cuadrática y su gráfico es una curva llamada parábola.
En la ecuación cuadrática sus términos se llaman:
si la ecuación tiene todos los términos se dice ecuación completa, si a la función le falta el término lineal o independiente se dice que la ecuación es incompleta.
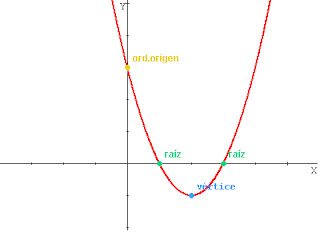
Estas curvas tienen ciertos elementos que la identifican como veremos en el siguiente gráfico
Raíces
Las raíces ( o ceros) de la función cuadrática son aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la parábola corta al eje x. Podemos ver a continuación que existen parábolas que cortan al eje x en:
lunes, 1 de noviembre de 2010
Definición: Función Lineal
una función lineal es una función polinómica de primer grado.una función que se representa en el plano cartesiano como una línea recta.
Esta función se puede escribir como
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Cuando cambiamos m modificamos la inclinación de la recta y cuando cambiamos b desplazamos la línea arriba o abajo.
Suscribirse a:
Comentarios (Atom)